Running Path of Exile 2 Simulations: Essence
Table of Contents

The Backstory: Why I Did This #
I’ve been playing this new game for a month now (Path of Exile 2) and to tackle the hardest content, you need really good gear, and to get that gear, you need a ton of in-game currency. The problem? The economy is wild. Players are constantly discovering new ways to farm currency, but as soon as a method gets popular, it stops being profitable.
As someone who loves programming and data (and maybe spends too much time thinking about spreadsheets), I thought: “Why not use my coding skills to figure out the best way to make currency?”
So, I set out to simulate currency conversion strategies in the game, specifically focusing on reforging essences to determine if I could find a profitable pattern, for instance, obtaining higher-tier essences that sell for the highest amount of currency (Exalted Orbs).
The Problem: Essence Reforging in PoE #
In PoE, “Essences” are crafting materials that can be reforged into higher-tier versions. The catch? Success rates are low, and outcomes are random. My question was simple:
If I reforged thousands of essences, would I turn a profit or go bankrupt?
To answer this, I built a Python simulator to model the process, incorporating:
- Conversion Probabilities: A 2.26% success rate for upgrades to a higher tier (from local and community data).
- Market Prices: Exalted Orb values for each essence type (spoiler: Greater Essence of Haste = $$$).
- Protected Resources: Some lower tier essences (e.g., Electricity) are too valuable to reforge.
Building the Simulator #
1. Modeling the Economy #
Real-World Limitations
Reforging essences comes with constraints that shape realistic simulations:
- Inventory Space: Players inventory and chest storage are limited.
- Market Volatility: Cheap essences are scarce in bulk, and prices fluctuate rapidly.
- Taxes: A transaction tax applies to marketplace sales in gold.
- Time: Reforging is time-consuming, and market shifts can erase profits.
Simulation Design
To mirror these challenges, the simulator:
- Runs 100,000 independent investment attempts (not endless reforging).
- Each attempt consist of 1000 reforges at the minimum. These many reforges equals to an affordable investment, reasonable inventory space, gold taxes and time consumed (25 minutes).
- Tracks metrics like average profit, loss streaks, and risk-adjusted returns.
Key Parameters
- Investment: 1,300 Exalted Orbs (avoids ruin in 95% of scenarios).
- Essence Input: 3,000 low-tier essences (2.3 Exalted each).
- Mechanics:
- Success (2.26%): Gain a random higher-tier essence.
- Failure: Receive one random minor essence (excluding protected Electricity/Haste).
# Simplified simulation loop
while reforges_possible:
consume_3_essences()
if success(probability=0.0226):
reward = random_greater_essence()
else:
refund = random_minor_essence()
2. Statistical Significance #
In PoE, reforging is a game of extremes. Most reforges grant you a low tier essence but a few can reward you with high-value essences like Greater Essence of Haste (worth 186 Exalted) or Greater Essence of the Infinite (worth 96 Exalted). Here’s the catch:
- Haste has a 0.1% drop rate. That means, on average, you’d need to reforge 1,000 times just to see one Greater Essence of Haste.
- Infinite has a 0.25% drop rate. Slightly better, but still rare.
In my early simulations, these rare events skewed the results. A single Haste drop could make an attempt look insanely profitable, while a streak of bad luck could wipe out my entire bankroll. This made it impossible to draw meaningful conclusions from even 100,000 attempts.
The Turning Point: Scaling Up #
To get reliable results, I realized I needed to simulate a lot more reforges.
-
Law of Large Numbers:
- The more trials you run, the closer your results will get to the true probabilities.
- With 100,000 attempts (100M reforges), I might see ~100,000 Haste drops. But with 1 million attempts (1 billion reforges), I’d expect ~1,000,000 Haste drops, giving a much clearer picture of their impact.
-
Reducing Variance:
- Small samples are noisy. By scaling up, I could smooth out the randomness and see the underlying trends.
-
Capturing Rare Events:
- Rare events like Haste drops dominate the profit distribution. Without enough trials, their impact is either overstated (if they happen early) or understated (if they don’t happen at all).
- Scaling up ensures these events are properly represented in the results.
So, I scaled up to 1 million simulations.
Results #
Average profit per attempt: 385 Exalted (95% CI: 384–386)
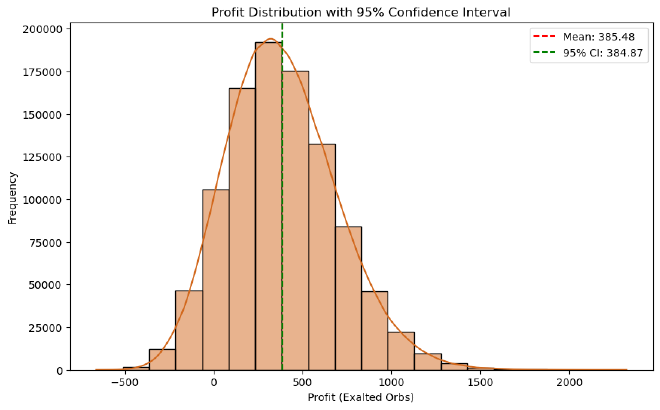
1. Profit Breakdown by Essence Type #
Minor Essence of Electricity is the most significant contributor, accounting for 30% of the total profit, followed by Greater Essence of Infinite and Greater Essence of Haste, contributing 18% and 15%, respectively. Despite being classified as a minor essence, minor Essence of Electricity has a larger impact than several greater essences.
| Essence | Profit Contribution | |
|---|---|---|
| 1 | Minor Essence of Electricity | 30% |
| 2 | Greater Essence of Infinite | 18% |
| 3 | Greater Essence of Haste | 15% |
| 4 | Greater Essence of Mind | 7% |
| 5 | Greater Essence of Electricity | 6% |
| 6 | Greater Essence of Sorcery | 6% |
| 7 | Greater Essence of Torment | 4% |
| 8 | Minor Essence of Haste | 3% |
| 9 | Greater Essence of Enhancement | 2% |
| 10 | Greater Essence of Battle | 1% |
2. Probability of Loss #
Formula: \(\text{Probability of Loss} = \frac{\text{Losing Attempts}}{\text{Total Attempts}} \)
\(\text{Probability of Loss} = 9.8\% \)
3. Win Rate / Loss Rate Ratio #
Formula: \( \text{ WL Ratio } = \frac{\text{Probability of Profit}}{\text{Probability of Loss}} \)
\( \text{ WL Ratio } = 9.20 \)
4. Value at Risk (VaR) #
Formula: \( \text{VaR} = \text{Percentile of Losses at Confidence Level} \)
\( \text{VaR}_{95\%}= 86.85 \text{ Exalted Orbs} \)
5. Risk-Adjusted Return (Sharpe Ratio) #
Formula: \(\text{Sharpe Ratio} = \frac{\text{Average Profit}}{\text{Standard Deviation of Profit}} \)
\(\text{Sharpe Ratio} = 1.24 \)
6. Expected Value (EV) per Attempt #
Formula: \({EV} = (\text{Average Profit} \times \text{Probability of Profit}) - (\text{Average Loss} \times \text{Probability of Loss}) \)
\({EV} = 358.68 \text{ Exalted Orbs } \)
Conclusion #
After simulating 1 million reforging attempts (1 billion reforges), the results are clear: reforging essences in Path of Exile 2 is a low-risk, high-reward strategy but only if you’re willing to spend 30 minutes repeating the same task. Here’s what the numbers tell us:
-
Profitability:
- Average Profit: 385 Exalted per attempt (95% CI: 384–386).
- Win/Loss Ratio: 9.2 (90.2% win rate vs. 9.8% loss rate).
- Expected Value: 358.68 Exalted per attempt.
-
Risk Management:
- Sharpe Ratio: 1.24.
- Value at Risk (VaR): 95% of attempts lose <86.85 Exalted.
-
Key Drivers:
- Electricity Essences: Contributed 30% of total profits.
- Haste & Infinite: Combined for 33.6% of profits, despite their rarity.
Thank you for reading! If you have any questions or comments, please feel free to contact me. Your feedback is highly appreciated.
Keywords: Python, Simulation, Path of Exile 2, Poe2